Detecting Alpha Particles from Thorium Decay

2022

Thorium-232 has a half life of 14.05 billion years — longer than the age of the universe. One gram of thorium contains 2.6e21 atoms, so despite its 4.43e17 second half life, you would expect to see 4060 decays per second per gram. Nearly all of these decays are alpha decays; thorium daughters that will also be present in any natural sample of thorium will emit beta and gamma radiation, but Th-232 produces no significant gamma on its own. Most Geiger counters are not sensitive to alpha particles, so just about everything that a Geiger counter picks up from a sample of thorium is from its daughters. The decay chain of thorium involves five additional alpha decays before reaching stable lead-208, so many of the detected alpha particles emitted by a natural sample of thorium are from the daughters and not from the thorium itself.

Original: Tosaka~commonswikiVector: BatesIsBack, CC BY-SA 3.0, via Wikimedia Commons

It's easy to detect alpha particles using a photodiode with an exposed die, so I ran two tests with thorium: one with a thoriated welding rod and one with thorium dioxide. You can buy thoriated welding rods on Amazon (thorium has a low work function which reduces electrode temperature in welding), and thorium dioxide powder encapsulated in plastic containers is sold on eBay as "check sources."

Setup

For both of these measurements, I used a picoammeter circuit modified to reverse bias the photodiode and AC couple that signal to the transimpedance amplifier (TIA). I also installed an OPA325 OP-AMP in place of LMP2231 and changed the feedback resistor to 10M to increase the response time. For counting the pulses, I used a Siglent SDS1104X-E oscilloscope.

Modified TIA Circuit

Thoriated Welding Rods

Thorium is added to some TIG welding rods because it has a lower work function (simplified: minimum energy required to remove an electron from the surface of the electrode) than tungsten. Tungsten has a work function of around 4.5 eV and thorium has a work function of around 3.5 eV. There is a small radiological hazard from welding with thorium containing rods, so, despite higher cost, TIG welding rods containing rare earth elements like Lanthanum are becoming more popular. Thoriated welding rods are not made from an alloy of thorium and tungsten — they are sintered together from powder. In fact, it isn't metallic thorium in these rods, its thorium dioxide.

Thoriated Welding Rods from Amazon

Typical thoriated welding rods contain 2% by weight thorium dioxide — about 0.14 grams for a 1.6 mm diameter 17.5 cm long rod. Thorium dioxide is 88% by weight thorium, so the rod contains about 0.12 grams of thorium. While the thorium in this rod will (ignoring daughters) produce \(4060*0.12=487 \) alphas per second, the number of alphas that escape the rod is much smaller because the rod shields most of them before they are able to escape. You can estimate the number of alphas that escape by simulating the penetration depth of the alphas through tungsten.

TRIM simulation of 4 MeV Alphas Impinging on Tungsten

Th-232 produces 3.95 and 4.01 MeV alphas. A quick TRIM simulation shows that most of these will make it through 5 µm of tungsten and that none of them make it past about 6.5 µm. Alphas are emitted randomly in all directions, so even an atom on the surface will only emit a detectable alpha half of time time since half of the time the alpha is emitted into the rod. For atoms between 0 and 5 µm into the rod, the fraction that escape can be determined by calculating the area of a spherical cap of a sphere with radius 5 µm centered below a plane approximating the surface of the rod.

Jhmadden, CC BY-SA 4.0 via Wikimedia Commons

The fraction of detectable alphas at a given depth is equal to the area of that cap divided by the total area of the sphere. The area of a spherical cap is \(A=2 \pi rh \), so the fraction of detectable alphas is: \[{{2 \pi r h} \over {4 \pi r^2}} = {{h} \over {2r}}\] To get an average over the 5 µm range of depths, you can express h as \(h=r-x\) where x is depth and apply the mean value theorem: \[{{1}\over{r}}\int_0^r {{r-x} \over {2r}} \,dx = {{1}\over{r}}\int_0^5 {{5-x} \over {10}} \,dx = {{5}\over{50}}\int_0^5 1 \,dx - {{1}\over{50}}\int_0^5 x \,dx = {{25}\over{50}} - {{12.5}\over{50}} = {{1}\over{4}}.\] This ignores the curvature of the rod, but 5 µm is << the 1.6 mm diameter of the rod.

The outer 5 µm of the rod is 0.6% the total volume of the rod, so only about \(487*0.006*0.25 = 0.73\) alphas per second escape a full 15cm rod. My photodiode detector has a limited area, though, so its detection rate will be much lower. I broke the rod into a 5mm long piece and taped that over the photodiode.

Left: Photodiode with Lens Removed. Right: Photodiode with Welding Rod

I found that it is easier to remove the glass lens from these diodes by placing the top of the diode in a vise and crushing it instead of cutting the body of the diode in half with a jeweler's saw. The walls of the package are 2.4mm above the surface of the die, and the area of the rod (I broke a small section off and taped it over the photodiode) that is visible by the die is 1.6 x 3.8mm. The thorium in the outer 5 µm of a plate of that area is about: \[m=1.6mm*3.8mm*0.005mm * {{1 cm^3} \over{1000 mm^3}} * 0.02 * 0.88 * {{19.3 g} \over{1 cm^3}} = 10 µg.\] That results in only 2.5 decays per minute. Not all of those will hit the photodiode. The photodiode has a sensor area of 0.78mm^2 while alphas that make it out of the visible part of the rod could end up going any direction under the rod. The area of a half sphere of radius 2.4mm is 36mm^2, so only 2.2% of the alphas that make it out of the visible part of the rod will hit the sensor. That brings the detection rate down to one per 18.55 minutes.

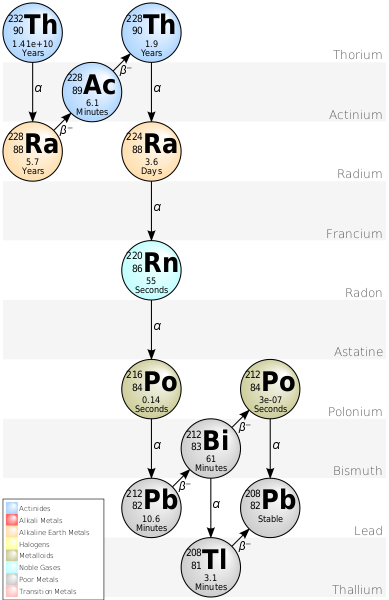
I connected the TIA to an oscilloscope in infinite persist mode and left it connected for 29 hours. The total number of events it counted was 110 which works out to one per 16 minutes. I am a bit surprised that the rate wasn't higher since my calculation neglected daughter products (the daughters of Th-232 emit five further alphas on their way to stable Pb-208). Still, its pretty cool to get a result within an order of magnitude of the estimated value. I hadn't bothered to run the calculation on how many alphas I expected to see per second before putting the setup together, so at first I thought that I had messed something up since I was waiting many minutes and not seeing anything. It was only after I set the scope to normal trigger mode and went to get coffee that I finally saw an event.

Stacked Events from Thoriated Welding Rod: 29 Hours

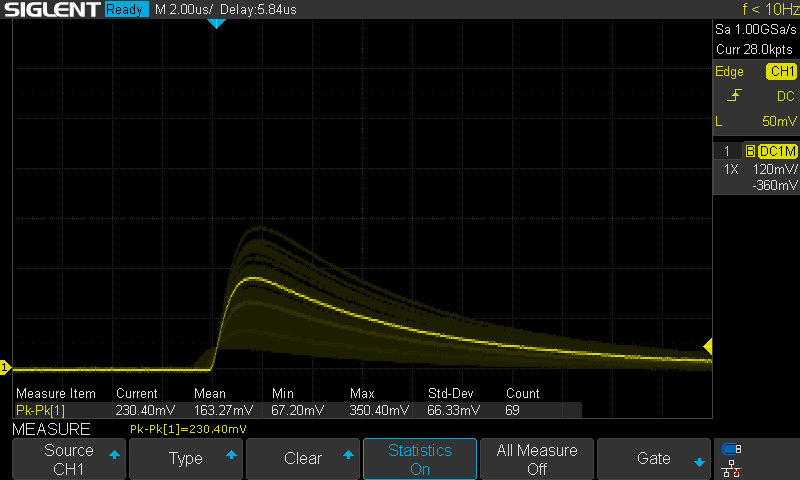
The peak amplitude in the above shot is significantly lower than what I later measured from thorium dioxide powder, but that is just due to a difference in in the feedback capacitance of the measurement circuits. I repeated this measurement after soldering the welding rod diode into same TIA circuit that I used for the powder and got much closer results. The thoriated welding rod has a peak pulse amplitude of 773mV and the thorium dioxide powder had a peak amplitude of 811mV. I captured 64 events over the 15.5 hours of this measurement which comes out ot one detection every 14.4 minutes.

Stacked Events from Thoriated Welding Rod: 15.5 Hours

The Poisson distribution can be used to model random discrete processes like radioactive decay. In a Poisson distribution, the variance is equal to the mean, so the standard deviation is the square root of the mean. For a single count (one-off) measurement, the standard deciation is the square root of the count. For 64 counts, the standard deviation is \(σ=\sqrt{64}=8 \). Expressed as rate, this is: \[σ_R={{\sqrt{64}}\over{t}}={{8}\over{930 min}}=0.0086 CPM \] From the definition of standard deviation, the probability that a the true rate is within two standard deviations of a measured rate 95.5%. This means that there is a 95.5% chance that the true rate of this sample is 0.069 ± 0.0086 CPM = 0.060-0.077 CPM.

Assuming that the thorium used to prepare these rods was chemically separated from ore shortly before the rods were manufactured, all the daughter products aside from thorium-228 would initially be missing. Since the half life of Ra-228 is about 3x longer than that of Th-228, the concentration of Th-228 will decrease for the first four or so years until sufficient Ra-228 builds up to replenish it. After 40 or so years, the ratio of daughter products will return to the natural equilibrium. Here's a chart of activity over time that I found in an old paper about the safety of thorium in gas mantles:

Thorium Activity After Initial Production

It would be interesting to empirically measure this by checking the activity of a thoriated rod every year for a few decades using a Geiger counter since it is the daughter products that emit beta and gamma radiation detectable by Geiger counters.

Thorium Dioxide Powder

Thorium dioxide powder isn't exactly something I want floating around my apartment (which is why I worked with it outside), but it is considered safe enough that the NRC allows it to be used in gas mantles that are handled by 12 year old boy scouts. Coleman phased out thorium in gas mantles for lanterns, but it is still used by some other brands and is still allowed by the NRC in 10 CFR 40.13(c)(1)(i) which is the same regulation permitting thorium to be used in welding rods. I'm not sure that selling plastic pucks full of it on eBay for use as a check source is strictly an allowed use for a commercial product, but the possession of up to 1.5 kg of thorium in powdered for is allowed by 10 CFR 40.22(a)(1). The applicability of this section to individuals is unclear since it refers to 'firms,' but, for perspective, some people manufacture yellowcake from uranium ore in their kitchen as a hobby.

Sketchy eBay Puck of Thorium Dioxide

To measure the alpha activity of the thorium dioxide relatively safely, I melted a hole in the bottom of the plastic puck that the thorium dioxide came in using a hot scalpel blade and then shook some out onto a sheet of aluminum foil and then taped the sample back up. I mixed the powder with rubbing alcohol to keep it from getting into the air as dust, and then packed it into a BPW24R photodiode with the glass lens removed and anti-reflective coating scrapped off. After letting that dry, I applied a few drops of cyanoacrylate glue to encapsulate the sample permanently.

"Randiode" — Photodiode Covered in Thorium Dioxide

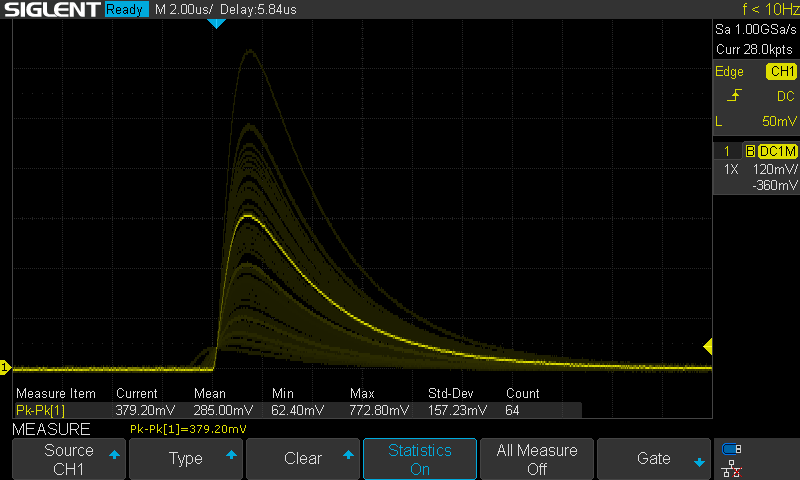
The result is a diode that detects about five alpha particles per minute. I recorded the output of the circuit with an oscilloscope for 1000 minutes and observed 5190 events. Here's the last 6.5 hours of measurement:

"Events Captured from 'Randiode'

The energy spectrum appears to be continuous which isn't surprising. The alphas are degraded as they pass through the bulk of the thorium dioxide and glue, so the characteristic peaks are spread broadly.