Satellite Nadir Angle and Slant Range Calculator

2025

The angles and distances between a satellite and a ground station are easy enough to calculate with trig, but I made this calculator to save me the trouble of re-deriving the equations every time.

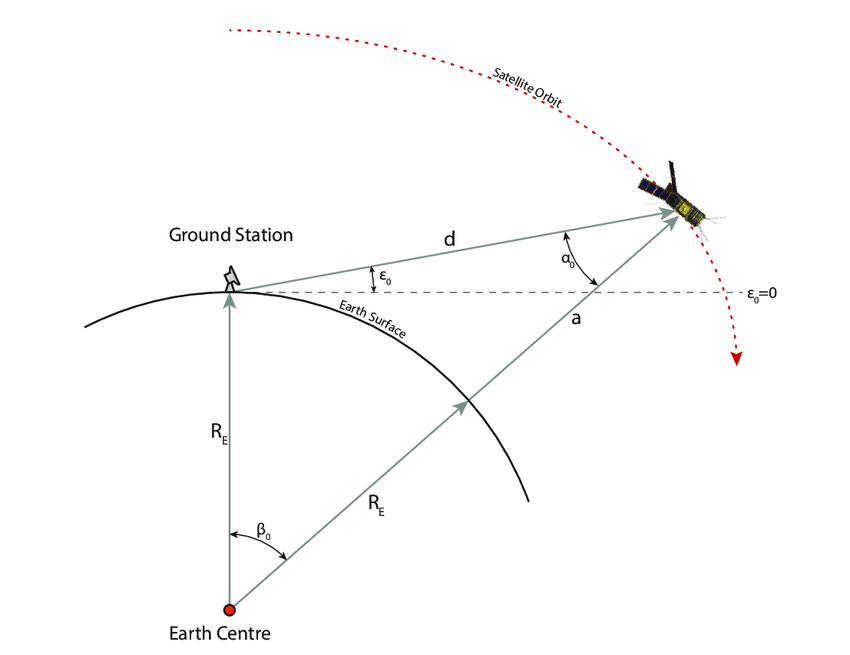
Diagram from here

I think the most intuitive way of solving this problem is to start with the law of sines:

$$\frac{sin(\alpha )}{R_e}=\frac{sin(\beta )}{d}=\frac{sin(90+ϵ)}{R_E+a}$$

If you are trying to calculate the satellite nadir angle α from elevation angle ε and altitude a, you can observe that:

$$\alpha =arcsin(R_E\cdot \frac{sin(90+ϵ)}{R_E+a})$$

Once you have that, you can calculate β easily from:

$$\beta =90-ϵ-\alpha$$

And you can plug β back into the law of sines relationship to determine d:

$$d=R_e\cdot \frac{sin(\beta )}{sin(\alpha )}$$

The portion of Earth's surface where the satellite is visible at this elevation angle and above can be determined by calculating the area of a spherical cap using the central angle β:

$$A=2\pi R_E^2(1-\cos (\beta ))$$

The distance along the earth's surface between the ground station and the point on the surface directly below the satellite is then given by:

$$d_s=R_e\cdot \beta \frac{\pi }{180}$$

Calculator